![]()
Aufgabe: Differenz gleich 5
Wie viele zweistellige natürliche Zahlen gibt es, bei denen die Differenz der beiden Ziffern gleich 5 ist?
Lösung anschauen: "+" klicken →
Es gibt neun dieser Zahlen, nämlich 16, 27, 38, 49, 50, 61, 72, 83 und 94.
![]()
Aufgabe: Rechenzeichen setzen
Setze auf der linken Seite Rechenzeichen derart, dass wahre Aussagen in Form von Gleichungen entstehen. Nebeneinanderstehende Ziffern dürfen als eine Zahl betrachtet, doch die Reihenfolge darf nicht geändert werden. Du darfst auch Klammern verwenden.
1 2 = 3
1 2 3 = 4
1 2 3 4 = 5
1 2 3 4 5 = 6
1 2 3 4 5 6 = 7
1 2 3 4 5 6 7 = 8
1 2 3 4 5 6 7 8 = 9
1 2 3 4 5 6 7 8 9 = 10
Lösung anschauen: "+" klicken →
Mögliche Lösung:
1 + 2 = 3
12 : 3 = 4
12 - 3 - 4 = 5
1 + 2 x 3 + 4 - 5 = 6
1 + 2 - 3 - 4 + 5 + 6 = 7
1 - 2 - 3 + 4 - 5 + 6 + 7 = 8
1 x 2 - 3 - 4 + 5 - 6 + 7 + 8 = 9
1 x 2 + 3 + 4 + 5 + 6 + 7 - 8 - 9 = 10
![]()
Multiplikationsaufgabe
Fränzchen hat sich eine interessante Aufgabe ausgedacht: Es sollen bei der Multiplikationsaufgabe
13# mal 7#= 1####
alle # so durch Ziffern ersetzt werden, dass
- alle drei Zahlen auf die gleiche Ziffer enden und dass
- beim Ergebnis an der Zehnerstelle die gleiche Ziffer steht wie an der Hunderterstelle.
Hinweis: das bedeutet natürlich, dass für # beim (fünfstelligen) Ergebnis unterschiedliche Ziffern eingesetzt werden können.
Lösung anschauen: "+" klicken →
Zu ersten Bedingung : Wenn alle drei Zahlen auf dieselbe Ziffer enden sollen, so heißt dies auch, dass das Produkt aus der letzten Ziffer (sie sei x genannt) mit sich selbst auf x enden muss. Also: x mal x = ...x
Daraus folgt: Mit der Forderung, dass x eine Ziffer ist, also 0 <= x <= 9 gilt, kommen nur noch
- x = 0,
- x = 1,
- x = 5 und
- x = 6
infrage. Bei allen anderen Ziffern käme am Ende beim Ergebnis eine andere Zahl raus (probiere es gerne aus).
Für diese 4 Fälle wird nun das Produkt gebildet:
- 130 • 70 = 9100 ist vierstellig und somit keine Lösung
- 131 • 71 = 9301 ist vierstellig und somit keine Lösung
- 135 • 75 = 10125 hat nicht dieselbe Zehner- und Hunderterstelle
- 136 • 76 = 10336 erfüllt alle Forderungen und ist somit einzige Lösung von Fränzchens' Multiplikationsaufgabe
![]()
Aufgabe: Mit dem Zug ins Ferienlager
Michael B. fuhr mit einem Sonderzug ins Zeltlager. Als der Zug genau die Hälfte seiner Reisestrecke zurückgelegt hatte, schlief Michael ein und erwachte erst, als der Zug noch eine Strecke von genau 25 km bis zum Reiseziel zurückzulegen hatte. Diese Strecke war halb so lang wie die Strecke, die der Zug zurückgelegt hatte, während Michael schlief.
Frage: Wie viel Kilometer betrug Michaels Reisestrecke?
Lösung anschauen: "+" klicken →
Die Gesamtstrecke werde mit x bezeichnet. Michael verschlief also eine Strecke von y = x/2 - 25 km. Da diese 25 km bis zum Ziel eine Strecke war, die halb so groß wie y war, gilt:
y = 2 · 25
x/2 - 25 = 50
x - 50 = 100
x = 150
Der Weg mit dem Zug ins Ferienlager war also für Michael 150 km lang.
Aufgabe: Vier Kisten
Vier gleich große Kisten mit gleichem Inhalt haben zusammen eine Masse von 132 kg.
Welche Masse hat dann der Inhalt einer Kiste, wenn die Masse aller vier leeren Kisten zusammen 12 kg beträgt?
Lösung anschauen: "+" klicken →
Wegen 132 - 12 = 120 beträgt die Gesamtmasse des Inhalts der vier Kisten 120 kg. Folglich beträgt wegen 120 : 4 = 30 die Masse des Inhalts je einer Kiste 30 kg.
![]()
Aufgabe: Quadratisches Netz 18
Gebe eine Möglichkeit an, die folgenden 16 Zahlen
1 / 1 / 2 / 2 / 3 / 3 / 4 / 4 / 5 / 5 / 6 / 6 / 7 / 7 / 8 / 8
so in die Felder des unten abgebildeten quadratischen (4x4-Kästchen) Netzes einzutragen, dass
- als Summe der Zahlen jeder Zeile (waagerecht),
- jeder Spalte (senkrecht),
- jeder der beiden Diagonalen (von links oben nach rechts unten und von rechts oben nach links unten) und
- als Summe der Zahlen in den vier Eckfeldern
die Zahl 18 erhalten wird.
Lösung anschauen: "+" klicken →
Mögliche Lösung:
![]()
Aufgabe: Der Schulgarten
Der Schulgarten einer Stadtschule hat einen Flächeninhalt von 0,15 ha (= Hektar. 1 ha = 10.000 m2). Der Garten wird in 9 Parzellen aufgeteilt, die einen Flächeninhalt von je 150 m2 bzw. 200 m2 besitzen.
Wie viele Parzellen von jeder der beiden Größen befinden sich im Garten?
Lösung anschauen: "+" klicken →
Lösung: Im Garten befinden sich 6 Parzellen zu je 150 m2 und 3 Parzellen zu je 200 m2.
Rechnung
1 ha = 10.000 m2
0,15 ha = 1.500 m2
1.500 ha = x * 150 m2 + y * 200 m2
x + y = 9
x = 9 - y
1.500 m2 = (9 - y) * 150 m2 + y * 200 m2
1.500 = 1.350 - 150 * y + 200 * y
150 = 50 * y
3 = y
Von oben: x = 9 - 3 = 6
x = 6
![]()
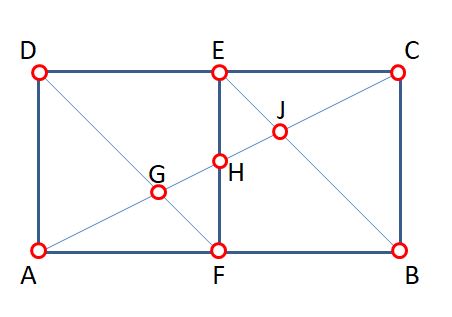
Aufgabe: Dreiecke suchen 1
Wie viele Dreiecke sind in der Figur enthalten?
Schreibe alle Dreiecke auf (z. B. ABC).
Lösung anschauen: "+" klicken →
Die Figur besteht aus insgesamt 8 Teilflächen, wovon folgende sechs Dreiecke sind:
AGD, AFG, GFH , EHJ, EJC und JBC.
Um weitere Dreiecke zu finden, untersuchen wir, ob Dreiecke aus zwei, drei, vier usw. benachbarten Teilflächen gebildet werden.
Aus zwei Teilflächen sind folgende sechs Dreiecke zusammengesetzt:
AFD, AFH, FED, EFB, EHC und EBC.
Aus drei Teilflächen sind es zwei Dreiecke: ABJ und DGC
und schließlich aus vier Teilflächen ebenfalls zwei Dreiecke: ABC und DAC.
Aus mehr als vier Teilflächen zusammengesetzt finden wir kein weiteres Dreieck. Somit sind in der Figur insgesamt 6 + 6 + 2 + 2 = 16 Dreiecke enthalten.
![]()
Aufgabe: LKW mit Schotter
Zum Transport einer bestimmten Menge Schotter hätte ein LKW mit 5 t Ladefähigkeit genau 105 vollbeladene Fuhren durchführen müssen. Nach 35 dieser Fuhren wurde er durch einen anderen LKW mit 7 t Ladefähigkeit abgelöst.
Berechne, wie viele vollbeladene Fuhren dieser zweite LKW noch durchzuführen hat, um die restliche Schottermenge abzutransportieren.
Lösung anschauen: "+" klicken →
Lösung: Es sind dann nur noch 50 weitere Fuhren (statt deren 70 mit dem 5-Tonner) notwendig.
Erste Lösungsmöglichkeit:
Wegen 105 x 5 = 525 waren insgesamt 525 t Schotter zu transportieren.
Wegen 35 x 5 = 175 hatte der erste LKW davon bis zu seiner Ablösung genau 175 t Schotter transportiert.
Mithin waren wegen 525 - 175 = 350 noch genau 350 t Schotter zu transportieren.
Wegen 350 : 7 = 50 konnte diese Menge von dem zweiten LKW mit genau 50 vollbeladenen Fuhren abtransportiert werden.
Zweite Lösungsmöglichkeit:
Wegen 105 - 35 = 70 hätte der erste LKW nach seiner Ablösung noch genau 70 Fuhren durchführen müssen.
Das war eine Schottermenge von 70 x 5 t. Die Anzahl der Fuhren des zweiten LKW ergibt sich, indem man die Anzahl dieser Tonnen durch 7 dividiert.
Man erhält 10 x 5 = 50. Also hat der zweite LKW noch genau 50 Fuhren durchzuführen.
![]()
Aufgabe: Summen bilden 1
Fülle eine Lösung für alle Zahlen (die Fragezeichen), bei der
- in jeder Zeile und in jeder Spalte die Teilsumme (= Summe alle Zahlen der Spalte/Zeile) 10 entsteht
- und die Summe aller acht Zahlen möglichst klein ist.
Hinweis: Die Fragezeichen können natürlich für unterschiedliche Zahlen stehen.
Lösung anschauen: "+" klicken →
![]()
Aufgabe: Geldgeschenk
Susanne erhält am 30. April zu ihrem Geburtstag von mehreren Verwandten Geld geschenkt. Sie hat nun genau 35 Euro in ihrer Spardose und nimmt sich vor, in den folgenden Monaten fleißig Altglas zu sammeln, so dass sie am Ende jedes Monats genau 5 Euro in die Spardose stecken kann.
Am Ende welchen Monats werden, wenn ihr dieses Vorhaben gelingt, erstmals 60 Euro in der Sparbüchse sein?
Lösung anschauen: "+" klicken →
Wegen 60 - 35 = 25 benötigt Kerstin zum Erreichen ihres Zieles noch genau 25 Euro. Da sie in jedem Monat 5 Euro sparen will, braucht sie wegen 25 : 5 = 5 noch genau 5 Monate dazu. Der fünfter Monat nach dem April ist der September. Die gewünschten 60 Euro werden also erstmals am Ende des Monats September in der Spardose sein.
![]()
Aufgabe: Summen bilden 2
In einem Schema wie im folgenden Bild sollen natürliche Zahlen eingetragen werden. Das folgende Bild zeigt ein Beispiel. Darin beträgt die Summe aller acht Zahlen 20. In jeder Zeile und in jeder Spalte entsteht dieselbe Teilsumme (=Summe der Zahlen in der Spalte bzw. Zeile), nämlich 7.
Bei der folgenden Aufgabe sind andere Zahlen gesucht. Gebe (wenn du kannst) zwei verschiedene mögliche Eintragungen bzw. Lösungen an, bei denen
- jeweils die Summe aller acht Zahlen 30 beträgt und
- in jeder Zeile sowie in jeder Spalte die Teilsumme 8 entsteht.
Lösung anschauen: "+" klicken →
Mögliche Lösungen wären:

Logisches Rätsel: Walnüsse
Susanne, Peter und Michael sehen auf dem Tisch einen Teller mit Walnüssen stehen. Sie wissen nicht, wie viele Nüsse es sind.
- Susanne meint: "Wenn man fünfmal nacheinander 19 Walnüsse vom Teller wegnimmt, bleiben noch mehr als 5 Walnüsse auf dem Teller zurück."
- Michael meint: "Wollte man aber fünfmal nacheinander 20 Walnüsse von dem Teller wegnehmen, so würden die Walnüsse dafür nicht ausreichen."
- Peter sagt: "Eine von euch beiden hat bestimmt recht."
Nach dem Auszählen wurde festgestellt, dass Peter sich geirrt hatte.
Frage: Wie viel Walnüsse lagen insgesamt auf dem Teller?
Lösung anschauen: "+" klicken →
- Susanne hatte wegen 5 x 19 + 5 = 100 gemeint, es seien mehr als 100 Walnüsse auf dem Teller gewesen.
- Michael hatte wegen 5 x 20 = 100 gemeint, es seien weniger als 100 Walnüsse gewesen.
- Da Peter sich geirrt hatte, hatte keines der beiden Mädchen recht.
Daher lagen genau 100 Walnüsse auf dem Teller.
![]()
Aufgabe: Summe darstellen
Definition vorab: Summand = Zahl bei einer Addition [Plusrechnung], die addiert wird.
Man kann jede natürliche Zahl 1, 2, 3, ... als eine Summe darstellen, in der jeder Summand eine 1 oder eine 2 ist.
Zum Beispiel gibt es für die Zahl 3 unter Beachtung der Reihenfolge genau die Darstellungen
3 = 1 + 1 + 1
= 1 + 2
= 2 + 1
Geben Sie für jede der Zahlen 4, 5 und 6 alle möglichen Additionen an.
Lösung anschauen: "+" klicken →
Die gesuchten Darstellungen sind:
4 = 1 + 1 + 1 + 1
= 1 + 1 + 2
= 1 + 2 + 1
= 2 + 1 + 1
= 2 + 2
5 = 1 + 1 + 1 + 1 + 1
= 1 + 1 + 1 + 2
= 1 + 1 + 2 + 1
= 1 + 2 + 1 + 1
= 2 + 1 + 1 + 1
= 1 + 2 + 2
= 2 + 1 + 2
= 2 + 2 + 1
6 = 1 + 1 + 1 + 1 + 1 + 1
= 1 + 1 + 1 + 1 + 2
= 1 + 1 + 1 + 2 + 1
= 1 + 1 + 2 + 1 + 1
= 1 + 2 + 1 + 1 + 1
= 2 + 1 + 1 + 1 + 1
= 1 + 1 + 2 + 2
= 1 + 2 + 1 + 2
= 1 + 2 + 2 + 1
= 2 + 1 + 1 + 2
= 2 + 1 + 2 + 1
= 2 + 2 + 1 + 1
= 2 + 2 + 2
Anmerkungen zur Lösung von Leserseite: Die Lösungen von Nr.14 sind meines Erachtens zu viele, da bei der Summe das Kommutativ- und Assoziativgesetz Gültigkeit hat, sind sowohl 2+1 als auch 1+2 gleich; ebenso 2+1+1 und 1+2+1 und 1+1+2; falls die Reihenfolge eine Rolle spielen sollte, müsste man die Aufgabe anders stellen, nämlich als Anzahl der Anordnungen (Kombinatorik).
![]()
Aufgabe: Junge Botaniker
Die Mitglieder einer Arbeitsgemeinschaft "Junge Botaniker" unterstützten ihre Paten beim Obstbau. Zu diesem Zwecke hielten sie eine 2,6 ha (ha = Hektar; 1 Hektar = 10.000 Quadratmeter) große Obstplantage, auf der je Hektar durchschnittlich 150 Apfelbäume standen, von Schädlingen frei. Danach wurden von jedem Baum durchschnittlich 50 kg Äpfel geerntet.
Berechnen Sie, wie viel Tonnen Äpfel unter diesen Umständen insgesamt auf der Plantage geerntet wurden.
Lösung anschauen: "+" klicken →
2,6 ha mit durchschnittlich 150 Bäumen je Hektar ergeben 2,6 x 150 = 390 Bäume.
Wenn durchschnittlich 50 kg Äpfel pro Baum geerntet wurden, so sind dies bei 390 Bäumen in Summe 19 500 kg Äpfel. Das sind umgerechnet 19,5 t Äpfel.
![]()
Aufgabe: Kryptogramm
Voarb die Definition vom Kryptogramm: Kryptogramm (früher: Geheimtext) bezeichnet heute ein mathematisches Rätsel bzw. eine Gleichung, deren Ziffern durch Buchstaben oder Zeichen ersetzt wurden. Das Ziel ist es, den Wert jeden Buchstabens/Zeichens zu finden.
Aufgabe
Gebe sämtliche Lösungen des nachstehenden Kryptogramms an, d. h. ersetze die Zeichen #,@,%,§ durch je eine der Ziffern 0 bis 9, dass zusammen mit den bereits angegebenen Ziffern sämtliche (waagerecht und senkrecht stehenden) Aufgaben richtig gelöst sind. Dabei bedeuten gleiche Zeichen gleiche Ziffern.
#@ + 8 = 3§
- - -
1% + § = 1§
------------------
1@ + 3 = #%
Lösung anschauen: "+" klicken →
Lösung
27 + 8 = 35
- - -
10 + 5 = 15
----------------
17 + 3 = 20
Lösungsweg:
- Das Zeichen % muss Null sein, da sonst die 1. Spalte keine wahre Aussage ergeben würde.
- Das Zeichen § muss den Wert 5 haben, da sonst die 2. Spalte keine wahre Aussage ergeben würde.
- Damit ergibt sich für # eine 2.
- Das Zeichen @ wird damit durch die dritte Zeile zu 7.
![]()
Rechenaufgabe: Olivenöl
Ein Behälter, der mit Olivenöl gefüllt ist, wiegt 17 kg 500 g. Der leere Behälter würde 2 kg 700 g wiegen.
- Wie viel Liter Öl befinden sich in dem Behälter, wenn 1 Liter Olivenöl 925 g wiegt?
- Für den Ladenverkauf wird das Öl in Flaschen zu 400 g abgefüllt. Wie viel Flaschen lassen sich mit dem im Behälter befindlichen Öl füllen?
Lösung anschauen: "+" klicken →
- Wegen 17 500 - 2 700 = 14 800 sind 14 kg 800 g Olivenöl im Behälter.
Aus 14 800 : 925 = 16 erhält man, dass sich 16 Liter Olivenöl im Behälter befinden. - Wegen 14 800 : 400 = 37 lassen sich 37 Flaschen mit der im Behälter vorhandenen Ölmenge füllen.
![]()
Aufgabe: Scherenschnitt
Kannst du die Figur mit einem Scherenschnitt (also die Figur einmal durchschneiden) so zerschneiden, dass die Teile zu einem Quadrat zusammengelegt werden können?
Finde bitte zwei verschiedene Möglichkeiten.
Tipp 1: Es ist gut, wenn man sich eine entsprechende Figur aus Papier ausschneidet und es damit versucht.
Tipp 2: Auch übereinanderlegen der zwei neuen Teile ist möglich.
Lösung anschauen: "+" klicken →
Zwei mögliche Schnitte wären:


![]()
Aufgabe: Wann treffen wir uns wieder?
"Genau eine Million zweihundertneuntausendsechshundert Sekunden dauert es, bis wir uns wieder treffen", sagt Michael, der gern mit großen Zahlen rechnet, zu Peter, als sie sich am 10. Mai um 12.00 Uhr verabschieden.
Wann treffen die beiden wieder zusammen?
Lösung anschauen: "+" klicken →
Die beiden treffen am 24. Mai 12.00 Uhr wieder zusammen.
1.209.600 Sekunden = 120.960/6 Minuten = 20.160 Minuten = 2.016/6 Stunden = 336 Stunden = 336/24 Tage = 14 Tage
10. Mai 12.00 Uhr + 14 Tage = 24. Mai 12.00 Uhr
![]()
Aufgabe: Radwanderung
Eine Gruppe von Schülern unternahm eine Radwanderung. Sie starteten innerhalb eines Ortes und erreichten nach 800 m Fahrt den Ortsausgang. Nachdem sie danach das Fünffache dieser Strecke zurückgelegt hatten, rasteten sie. Nach weiteren 14 km machten sie Mittagspause. Die Reststrecke bis zu ihrem Fahrtziel betrug 2,5 km weniger als die bisher zurückgelegte Strecke.
Ermittele die Gesamtlänge der Strecke vom Start bis zum Ziel!
Lösung anschauen: "+" klicken →
Lösung: Das sind 35 km und 100 m.
Lösungsweg:
- s = 800 m + 4.000 m + 14.000 m + 800 m + 4.000 m + 14.000 m - 2.500 m
- s = 2 x (800 m + 4.000 m + 14.000 m) - 2.500 m
- s = 37.600 - 2.500
- s = 35.100 m
Umfrage
Hast du eine Anmerkung zu obigen Lösungen (Korrektur oder weitere mögliche Lösung)?
Quellenangabe: Rätsel wurden großenteils inspiriert von https://www.olympiade-mathematik.de.
Möchtest du ein Mathe-Rätsel mit Lösung ergänzen?
Vielen Dank!